Investigation#

First, let’s explore our data.

idot = pd.read_csv('../../data/idot_abbrv.csv')
idot.head()

	year	reason	driver_race	beat	district
0	2019	moving	black	215	2
1	2019	equipment	white	2422	24
2	2019	moving	black	1522	15
3	2019	moving	black	2432	24
4	2019	moving	hispanic	2423	24

idot.shape

(925805, 7)

Our dataset has 7 columns and 925,805 rows where each row is a traffic stop that occurred in Chicago.

The 7 variables can be described as follows:

year - the year the traffic stop happened
reason - the reason for the stop, one of: moving, equipment, license, or none
any_search - a boolean variable indicating whether (1) or not (0) the car or any of its passengers were searched during the traffic stop
search_hit - a boolean variable indicating whether (1) or not (0) anything illegal was found during a search (value is 0 if no search was conducted)
driver_race - perceived race of the driver as reported by the officer, one of: black, white, hispanic, asian, am_indian, or other
beat - the police beat in which the traffic stop occurred (first 2 digits indicate the surrounding police district)
district - the police district in which the traffic stop occurred

Let’s look at these variables more closely.

idot.year.unique()

array([2019, 2020])

Using .unique, we can see that the dataset includes stops from the years 2019-2020, but we are only interested in 2020. Let’s filter the data so that we only have data for 2020.

idot_20 = idot.loc[idot.year == 2020].reset_index(drop=True)
idot_20.head()

	year	reason	driver_race	beat	district
0	2020	moving	am_indian	1024	10
1	2020	moving	hispanic	433	4
2	2020	equipment	black	1021	10
3	2020	equipment	black	735	7
4	2020	moving	black	2011	20

idot_20.shape

(327290, 7)

Now, we have 327,290 stops in our data. There is a lot of interesting data here including whether the car was searched, if the officer found contraband (called a ‘hit’), and where the stop occurred (the police district and beat). For example, Hyde Park is in district 2. Let’s see how many stops occurred in district 2.

idot_20.groupby("district")["reason"].count()

district
    9347
   15905
   14510
   20800
    8567
   11035
   27101
   17449
   12383
  24979
  41736
  14788
   8468
  24066
   4575
   7994
   9588
   7132
   8118
   5729
   7542
  23515
   1963
Name: reason, dtype: int64

So, there were 15,905 traffic stops made in the district surrounding Hyde Park in 2020.

We can create a histogram to see the distribution of numbers of stops per police beat.

plt.hist(idot_20.groupby("beat")["reason"].count());
plt.xlabel("Number of Traffic Stops")
plt.ylabel("Frequency")
plt.title("Distribution of Traffic Stops By Beat")
plt.show()

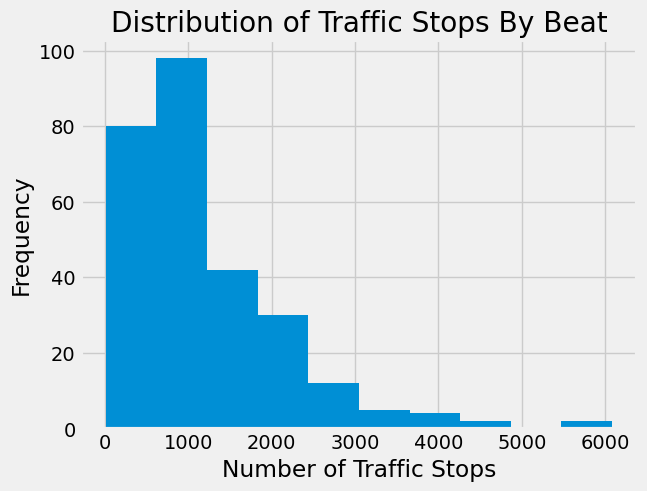
This shows that there is a wide range of numbers of stops in each police beat.The variability we see is likely due to a number of factors including unequal population and land area between beats as well as differing road size and traffic levels.

Two beats have around 6,000 stops, more than any other beat in 2020. Let’s identify those beats.

stop_counts = idot_20.groupby("beat")[["reason"]].count()
stop_counts[stop_counts.reason > 5000]

	reason
beat
1112	6081
1533	5875

Upon inspection, these beats are both west of downtown Chicago and beat 1533 contains part of interstate 290.

We can also investigate the reason for the traffic stops.

idot_20.groupby("reason")["district"].count()

reason
equipment    131250
license       66398
moving       129638
none              4
Name: district, dtype: int64

In 2020, 129,638 people were stopped for moving violations (like speeding or not using a blinker), 131,250 were stopped because of equipment (like a burnt out taillight), 66,398 were stopped for an invalid license, and there were 4 cases where the reason was not entered in the database.

Traffic Stops#

This is all very interesting, but we wanted to investigate the stop rates for drivers of different races. We can do this using the variable driver_race. First, let’s drop some of the columns that we don’t need for now.

idot_20_abbrv = idot_20.drop(columns=["reason","beat","district"])
idot_20_abbrv

	year	any_search	search_hit	driver_race
0	2020	0	0	am_indian
1	2020	0	0	hispanic
2	2020	0	0	black
3	2020	0	0	black
4	2020	0	0	black
...	...	...	...	...
327285	2020	0	0	asian
327286	2020	0	0	black
327287	2020	0	0	white
327288	2020	0	0	black
327289	2020	0	0	hispanic

327290 rows × 4 columns

Recall, we also could have selected only the columns we wanted instead of dropping the columns we didn’t need (see Chapter 6).

Now, let’s group the data by driver_race and count how many drivers of each race were stopped in 2020.

stopped = idot_20_abbrv.groupby("driver_race")["year"].count().reset_index().rename(columns={"year":"num_stopped"})
stopped

	driver_race	num_stopped
0	am_indian	1176
1	asian	7448
2	black	204203
3	hispanic	78449
4	other	895
5	white	35053

From this table, it certainly looks like more Black and Hispanic drivers were stopped in 2020 than drivers of other races. However, we are only looking at raw counts. It will be easier to see a pattern if we convert these counts to a proportion of total stops and then visualize the data.

stopped['prop_stopped'] = np.round(stopped['num_stopped'] / 327290, decimals=4)
stopped

	driver_race	num_stopped	prop_stopped
0	am_indian	1176	0.0036
1	asian	7448	0.0228
2	black	204203	0.6239
3	hispanic	78449	0.2397
4	other	895	0.0027
5	white	35053	0.1071

plt.bar(stopped['driver_race'], stopped["prop_stopped"])
plt.xlabel("Driver's Race")
plt.ylabel("Proportion of Stops")
plt.show()

From this figure, we can see that approximately 62% of drivers stopped were Black, 24% were Hispanic, and 11% were White.

The Benchmark#

In order to do a benchmark analysis, we need a benchmark for comparison, in this case, the population of Chicago. Next, we will read-in data on the estimated driving population of each race by beat. This dataset was created by a research team at the University of Chicago Data Science Institute.

Note that these benchmark populations are not integers. This data was estimated probabilistically using data on age and race of drivers (see the explanation in the previous section) which resulted in continuous estimates.

pop = pd.read_csv('../../data/adjusted_population_beat.csv')
pop[["White","Black","Hispanic","Asian","Native","Other"]] = pop[["White","Black","Hispanic","Asian","Native","Other"]].apply(np.round, decimals=4)
pop.head()

	beat	White	Black	Hispanic	Asian	Native
0	1713	1341.0698	1865.3001	937.4999	317.0765	0.0000
1	1651	0.0000	0.0000	0.0000	0.0000	0.0000
2	1914	641.2881	5878.7811	1621.2010	407.4879	0.0000
3	1915	1178.3223	1331.1240	1597.0273	283.1750	0.0000
4	1913	739.5932	2429.8962	535.7215	121.0840	159.0156

Since, we are interested in Chicago as a whole, we can sum over beats to get the estimated population for all of Chicago.

pop_total = pop.sum(axis=0).to_frame(name="est_pop").reset_index().rename(columns={'index': 'driver_race'})
pop_total

	driver_race	est_pop
0	beat	335962.0000
1	White	298755.1974
2	Black	248709.5311
3	Hispanic	222341.2245
4	Asian	60069.7684
5	Native	2664.8764
6	Other	212.5375

Clearly, the beat row gives us no useful information, so let’s drop it.

pop_total = pop_total.drop([0])
pop_total

	driver_race	est_pop
1	White	298755.1974
2	Black	248709.5311
3	Hispanic	222341.2245
4	Asian	60069.7684
5	Native	2664.8764
6	Other	212.5375

Now, we can calculate proportions of the population, similar to what we did with number of traffic stops above.

pop_total['prop_pop'] = np.round(pop_total['est_pop'] / pop_total['est_pop'].sum(), decimals=4)
pop_total

	driver_race	est_pop	prop_pop
1	White	298755.1974	0.3588
2	Black	248709.5311	0.2987
3	Hispanic	222341.2245	0.2670
4	Asian	60069.7684	0.0721
5	Native	2664.8764	0.0032
6	Other	212.5375	0.0003

We want to compare these proportions with the proportion of stops we calculated above. This is easier to do if they are in the same DataFrame. We can combine them using merge, but first, we need to make sure each race has the same name in both DataFrames. One DataFrame has races capitalized, while the other is all lowercase. Also, one DataFrame uses the shortened term ‘native’ while the other uses ‘am_indian’. Let’s use .apply and .replace to fix this.

def to_lowercase(x):
    '''A function that takes in a string and returns that string converted to all lowercase letters'''
    return x.lower()

pop_total['driver_race'] = pop_total['driver_race'].apply(to_lowercase)
pop_total

	driver_race	est_pop	prop_pop
1	white	298755.1974	0.3588
2	black	248709.5311	0.2987
3	hispanic	222341.2245	0.2670
4	asian	60069.7684	0.0721
5	native	2664.8764	0.0032
6	other	212.5375	0.0003

The .replace method can be used along with a dictionary to map values from a series onto different values. In this case, we are mapping all occurrences of ‘native’ to ‘am_indian’.

race_map = {"native":"am_indian"}

pop_total['driver_race'] = pop_total['driver_race'].replace(race_map)
pop_total

	driver_race	est_pop	prop_pop
1	white	298755.1974	0.3588
2	black	248709.5311	0.2987
3	hispanic	222341.2245	0.2670
4	asian	60069.7684	0.0721
5	am_indian	2664.8764	0.0032
6	other	212.5375	0.0003

stops_vs_pop = stopped.merge(pop_total)
stops_vs_pop

	driver_race	num_stopped	prop_stopped	est_pop	prop_pop
0	am_indian	1176	0.0036	2664.8764	0.0032
1	asian	7448	0.0228	60069.7684	0.0721
2	black	204203	0.6239	248709.5311	0.2987
3	hispanic	78449	0.2397	222341.2245	0.2670
4	other	895	0.0027	212.5375	0.0003
5	white	35053	0.1071	298755.1974	0.3588

x = np.arange(len(stops_vs_pop.driver_race))  # the label locations
width = 0.44  # the width of the bars

fig, ax = plt.subplots()

rects1 = ax.bar(x, round(stops_vs_pop.prop_stopped,2), width, label="Proportion of Stops")
ax.bar_label(rects1, padding=4)

rects2 = ax.bar(x + width, round(stops_vs_pop.prop_pop,2), width, label="Proportion of Population")
ax.bar_label(rects2, padding=4)

# Add some text for labels, title and custom x-axis tick labels, etc.
ax.set_ylabel('Proportion of Stops/Population')
ax.set_xlabel("Driver's Race")
ax.set_title('Traffic Stops by Race')
ax.set_xticks(x + width/2, stops_vs_pop.driver_race)
ax.legend(loc=4, bbox_to_anchor=(1.3, 0.7))

plt.show()

Using this figure, we can see that American Indian, Hispanic, and Other drivers are all stopped at a proportion that is similar to the proportion of the population they make up. However, Black drivers are stopped twice as often as we would expect to see according to their population, and Asian and White drivers are stopped at rates less than their proportion of the population.

Searches#

Our data doesn’t just have information on stops. It also has information on whether the driver or car were searched during the traffic stop. Let’s investigate searches and hits by race as well. This type of investigation is called an outcomes analysis since we are comparing the outcomes (hits) of searches.

searched = idot_20_abbrv.groupby("driver_race")[["any_search","search_hit"]].sum().reset_index().rename(columns={"any_search":"num_searched", "search_hit":"num_hit"})
searched

	driver_race	num_searched	num_hit
0	am_indian	3	1
1	asian	31	12
2	black	3712	980
3	hispanic	1140	317
4	other	5	3
5	white	190	66

Again, let’s convert counts to proportions. For number of searches, we will convert to proportion of total searches. For number of hits, we will convert to proportion of searches that resulted in a hit.

searched['prop_searched'] = np.round(searched['num_searched'] / searched['num_searched'].sum(), decimals=4)
searched

	driver_race	num_searched	num_hit	prop_searched
0	am_indian	3	1	0.0006
1	asian	31	12	0.0061
2	black	3712	980	0.7306
3	hispanic	1140	317	0.2244
4	other	5	3	0.0010
5	white	190	66	0.0374

plt.bar(searched['driver_race'], searched["prop_searched"])
plt.xlabel("Driver's Race")
plt.ylabel("Proportion of Searches")
plt.show()

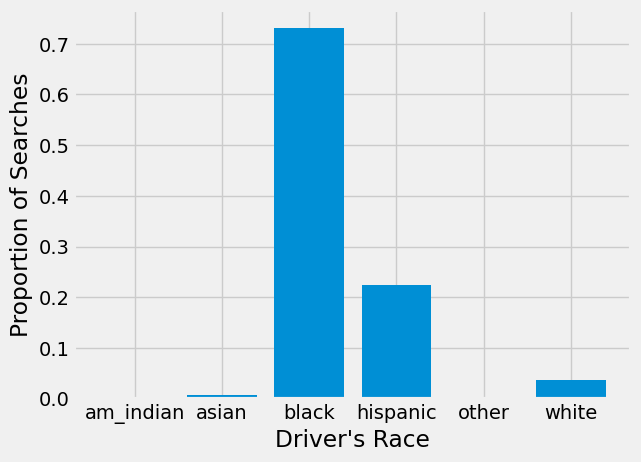
We can see from this barchart that Black drivers are searched much more often than drivers of any other race. Over 70% of searches conducted in 2020 were of Black drivers!

Are these searches successful? If these were necessary searches, officers should be finding contraband more often when searching Black drivers.

searched['prop_hit'] = np.round(searched['num_hit'] / searched['num_searched'], decimals=4)
searched

	driver_race	num_searched	num_hit	prop_searched	prop_hit
0	am_indian	3	1	0.0006	0.3333
1	asian	31	12	0.0061	0.3871
2	black	3712	980	0.7306	0.2640
3	hispanic	1140	317	0.2244	0.2781
4	other	5	3	0.0010	0.6000
5	white	190	66	0.0374	0.3474

plt.bar(searched['driver_race'], searched["prop_hit"])
plt.xlabel("Driver's Race")
plt.ylabel("Proportion of Successful Searches")
plt.show()

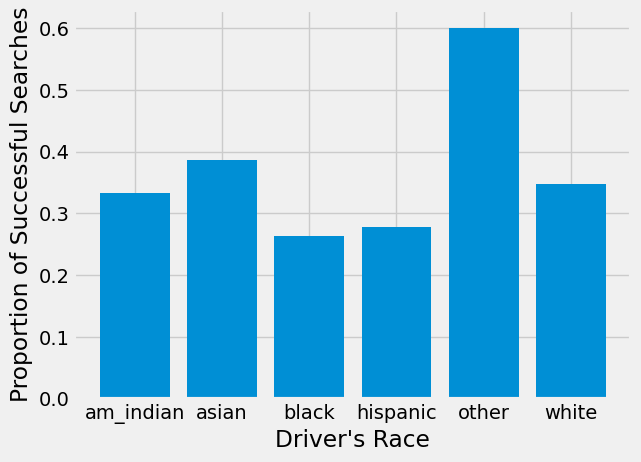
American Indian, Asian, and other drivers all have small numbers of searches. Focusing on the 3 races with enough searches to analyze, we see that, despite being searched more often, searches of Black drivers result in a hit slightly less often than searches of White drivers.

We see a slightly taller bar for White drivers in the previous barchart. It would be interesting to know if contraband is found on White drivers significantly more often than Black drivers. Let’s add a confidence interval to the point estimates shown in the plot. We will focus on the three most common races in our data: Black, Hispanic, and White.

First, we create 1000 bootstrap samples and calculate hit proportions for White, Black, and Hispanic drivers in each sample.

props_white = np.array([])
props_black = np.array([])
props_hispanic = np.array([])
for i in np.arange(1000):
    bootstrap_sample = idot_20_abbrv.sample(len(idot_20_abbrv),replace=True)
    searches = bootstrap_sample.groupby("driver_race")[["any_search","search_hit"]].sum().reset_index().rename(columns={"any_search":"num_searched", "search_hit":"num_hit"})
    searches['prop_hit'] = searches['num_hit'] / searches['num_searched']
    resampled_white = searches[searches.driver_race == "white"]["prop_hit"]
    resampled_black = searches[searches.driver_race == "black"]["prop_hit"]
    resampled_hispanic = searches[searches.driver_race == "hispanic"]["prop_hit"]
    props_white = np.append(props_white, resampled_white)
    props_black = np.append(props_black, resampled_black)
    props_hispanic = np.append(props_hispanic, resampled_hispanic)

white_ci = np.percentile(props_white, [2.5,97.5])
black_ci = np.percentile(props_black, [2.5,97.5])
hispanic_ci = np.percentile(props_hispanic, [2.5,97.5])

---------------------------------------------------------------------------
KeyboardInterrupt                         Traceback (most recent call last)
Cell In[28], line 6
for i in np.arange(1000):
   bootstrap_sample = idot_20_abbrv.sample(len(idot_20_abbrv),replace=True)
----> 6     searches = bootstrap_sample.groupby("driver_race")[["any_search","search_hit"]].sum().reset_index().rename(columns={"any_search":"num_searched", "search_hit":"num_hit"})
   searches['prop_hit'] = searches['num_hit'] / searches['num_searched']
   resampled_white = searches[searches.driver_race == "white"]["prop_hit"]

File /opt/conda/lib/python3.11/site-packages/pandas/core/groupby/groupby.py:3052, in GroupBy.sum(self, numeric_only, min_count, engine, engine_kwargs)
else:
   # If we are grouping on categoricals we want unobserved categories to
   # return zero, rather than the default of NaN which the reindexing in
   # _agg_general() returns. GH #31422
   with com.temp_setattr(self, "observed", True):
-> 3052         result = self._agg_general(
           numeric_only=numeric_only,
           min_count=min_count,
           alias="sum",
           npfunc=np.sum,
       )
   return self._reindex_output(result, fill_value=0)

File /opt/conda/lib/python3.11/site-packages/pandas/core/groupby/groupby.py:1834, in GroupBy._agg_general(self, numeric_only, min_count, alias, npfunc)
@final
def _agg_general(
   self,
   (...)
   npfunc: Callable,
):
-> 1834     result = self._cython_agg_general(
       how=alias,
       alt=npfunc,
       numeric_only=numeric_only,
       min_count=min_count,
   )
   return result.__finalize__(self.obj, method="groupby")

File /opt/conda/lib/python3.11/site-packages/pandas/core/groupby/groupby.py:1925, in GroupBy._cython_agg_general(self, how, alt, numeric_only, min_count, **kwargs)
   result = self._agg_py_fallback(how, values, ndim=data.ndim, alt=alt)
   return result
-> 1925 new_mgr = data.grouped_reduce(array_func)
res = self._wrap_agged_manager(new_mgr)
out = self._wrap_aggregated_output(res)

File /opt/conda/lib/python3.11/site-packages/pandas/core/internals/managers.py:1431, in BlockManager.grouped_reduce(self, func)
           result_blocks = extend_blocks(applied, result_blocks)
   else:
-> 1431         applied = blk.apply(func)
       result_blocks = extend_blocks(applied, result_blocks)
if len(result_blocks) == 0:

File /opt/conda/lib/python3.11/site-packages/pandas/core/internals/blocks.py:366, in Block.apply(self, func, **kwargs)
@final
def apply(self, func, **kwargs) -> list[Block]:
   """
   apply the function to my values; return a block if we are not
   one
   """
--> 366     result = func(self.values, **kwargs)
   result = maybe_coerce_values(result)
   return self._split_op_result(result)

File /opt/conda/lib/python3.11/site-packages/pandas/core/groupby/groupby.py:1901, in GroupBy._cython_agg_general.<locals>.array_func(values)
def array_func(values: ArrayLike) -> ArrayLike:
   try:
-> 1901         result = self.grouper._cython_operation(
           "aggregate",
           values,
           how,
           axis=data.ndim - 1,
           min_count=min_count,
           **kwargs,
       )
   except NotImplementedError:
       # generally if we have numeric_only=False
       # and non-applicable functions
       # try to python agg
       # TODO: shouldn't min_count matter?
       # TODO: avoid special casing SparseArray here
       if how in ["any", "all"] and isinstance(values, SparseArray):

File /opt/conda/lib/python3.11/site-packages/pandas/core/groupby/ops.py:811, in BaseGrouper._cython_operation(self, kind, values, how, axis, min_count, **kwargs)
"""
Returns the values of a cython operation.
"""
assert kind in ["transform", "aggregate"]
--> 811 cy_op = WrappedCythonOp(kind=kind, how=how, has_dropped_na=self.has_dropped_na)
ids, _, _ = self.group_info
ngroups = self.ngroups

File properties.pyx:36, in pandas._libs.properties.CachedProperty.__get__()

File /opt/conda/lib/python3.11/site-packages/pandas/core/groupby/ops.py:725, in BaseGrouper.has_dropped_na(self)
@final
@cache_readonly
def has_dropped_na(self) -> bool:
   """
   Whether grouper has null value(s) that are dropped.
   """
--> 725     return bool((self.group_info[0] < 0).any())

File properties.pyx:36, in pandas._libs.properties.CachedProperty.__get__()

File /opt/conda/lib/python3.11/site-packages/pandas/core/groupby/ops.py:729, in BaseGrouper.group_info(self)
@cache_readonly
def group_info(self) -> tuple[npt.NDArray[np.intp], npt.NDArray[np.intp], int]:
--> 729     comp_ids, obs_group_ids = self._get_compressed_codes()
   ngroups = len(obs_group_ids)
   comp_ids = ensure_platform_int(comp_ids)

File /opt/conda/lib/python3.11/site-packages/pandas/core/groupby/ops.py:753, in BaseGrouper._get_compressed_codes(self)
   # FIXME: compress_group_index's second return value is int64, not intp
ping = self.groupings[0]
--> 753 return ping.codes, np.arange(len(ping.group_index), dtype=np.intp)

File /opt/conda/lib/python3.11/site-packages/pandas/core/groupby/grouper.py:691, in Grouping.codes(self)
@property
def codes(self) -> npt.NDArray[np.signedinteger]:
--> 691     return self._codes_and_uniques[0]

File properties.pyx:36, in pandas._libs.properties.CachedProperty.__get__()

File /opt/conda/lib/python3.11/site-packages/pandas/core/groupby/grouper.py:801, in Grouping._codes_and_uniques(self)
   uniques = self._uniques
else:
   # GH35667, replace dropna=False with use_na_sentinel=False
   # error: Incompatible types in assignment (expression has type "Union[
   # ndarray[Any, Any], Index]", variable has type "Categorical")
--> 801     codes, uniques = algorithms.factorize(  # type: ignore[assignment]
       self.grouping_vector, sort=self._sort, use_na_sentinel=self._dropna
   )
return codes, uniques

File /opt/conda/lib/python3.11/site-packages/pandas/core/algorithms.py:795, in factorize(values, sort, use_na_sentinel, size_hint)
           # Don't modify (potentially user-provided) array
           values = np.where(null_mask, na_value, values)
--> 795     codes, uniques = factorize_array(
       values,
       use_na_sentinel=use_na_sentinel,
       size_hint=size_hint,
   )
if sort and len(uniques) > 0:
   uniques, codes = safe_sort(
       uniques,
       codes,
   (...)
       verify=False,
   )

File /opt/conda/lib/python3.11/site-packages/pandas/core/algorithms.py:595, in factorize_array(values, use_na_sentinel, size_hint, na_value, mask)
hash_klass, values = _get_hashtable_algo(values)
table = hash_klass(size_hint or len(values))
--> 595 uniques, codes = table.factorize(
   values,
   na_sentinel=-1,
   na_value=na_value,
   mask=mask,
   ignore_na=use_na_sentinel,
)
# re-cast e.g. i8->dt64/td64, uint8->bool
uniques = _reconstruct_data(uniques, original.dtype, original)

KeyboardInterrupt: 

Now that we have our three 95% bootstrap confidence intervals, we need to get them in the correct format to make error bars on our graph. The method .T transposes a 2-D array or matrix. In this case, we need all lower limits in one row and all upper limits in another, so we transpose our array and then make it back into a list. The argument that creates error bars also needs the upper and lower limits in the format of distances from the top of the bar in a barchart so we subtract to find those distances.

searched3 = searched.loc[searched.driver_race.isin(['white','black','hispanic'])]

errors = np.array([black_ci, hispanic_ci, white_ci]).T.tolist()
low = searched3["prop_hit"] - errors[0]
high = errors[1] - searched3["prop_hit"]

Now, we can plot our barchart and include the confidence interval we calculated.

plt.bar(searched3['driver_race'], searched3["prop_hit"], yerr=[low,high], capsize=10)
plt.xlabel("Driver's Race")
plt.ylabel("Proportion of Successful Searches")
plt.show()

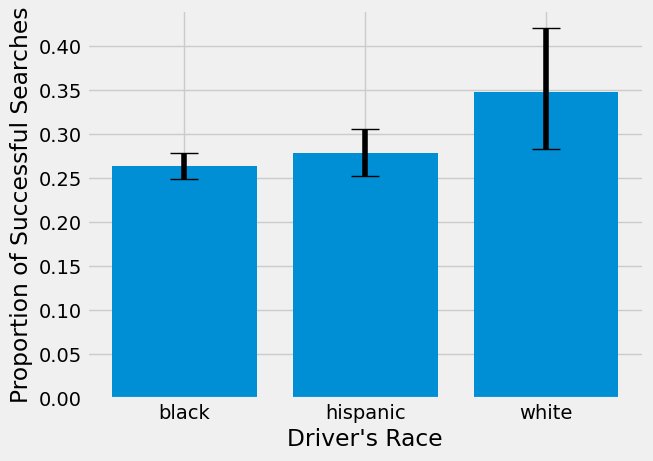
The 95% bootstrap confidence intervals for Black and Hispanic and Hispanic and White seem to overlap, but those for Black and White don’t, indicating there is a significant difference between the two. Let’s double check this with a hypothesis test for the difference in proportion of successful searches between Black and White drivers.

We will conduct a two-sided permutation test. The null hypothesis for our test is that there is no difference in proportion of successful searches between Black and White drivers. Our alternative hypothesis is that there is a difference.

np.random.seed(42)
differences = np.array([])
shuffled_dat = idot_20_abbrv.loc[idot_20_abbrv.driver_race.isin(['white','black'])].copy()

for i in np.arange(1000):
    shuffled_dat['shuffled_races'] = np.random.permutation(shuffled_dat["driver_race"])
    shuffle_searched = shuffled_dat.groupby("shuffled_races")[["any_search","search_hit"]].sum().reset_index().rename(columns={"any_search":"num_searched", "search_hit":"num_hit"})
    shuffle_searched['prop_hit'] = shuffle_searched['num_hit'] / shuffle_searched['num_searched']
    diff = shuffle_searched.loc[shuffle_searched['shuffled_races'] == 'white','prop_hit'].iloc[0] - shuffle_searched.loc[shuffle_searched['shuffled_races'] == 'black','prop_hit'].iloc[0]
    differences = np.append(differences, diff)

data_diff = searched3.loc[searched3['driver_race'] == 'white','prop_hit'].iloc[0] - searched3.loc[searched3['driver_race'] == 'black','prop_hit'].iloc[0]
plt.hist(differences)
plt.scatter(data_diff, -1, color='red', s=30)
plt.title('1000 simulated datasets');
plt.xlabel("Difference in proportions of hits");
plt.ylabel("Frequency");

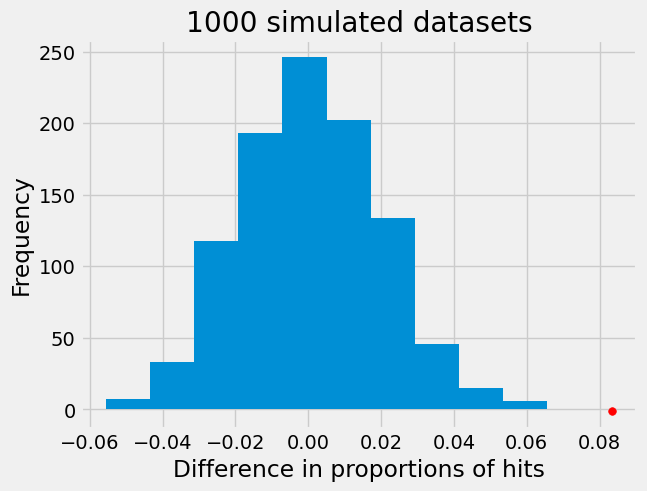
Our permutation test shows that the difference in proportions we see in our data is not consistent with what we would expect if there was no difference between the two groups. In fact, the red dot does not overlap with our histogram at all indicating our p-value is 0. So, we can reject the null hypothesis that Black and White drivers have similar proportions of search hits, and conclude that contraband is found on Black drivers at a significantly lower rate than White drivers!

Conclusions#

We’ve showed two different strategies for investigating racial bias: benchmarking and outcomes analysis. Both strategies have been used by real data scientists in cities like Chicago, Nashville, and New York to detect biased police practices.

This case study shows that you can answer important data science questions with the information you have learned so far in this book. Skills like grouping and merging, creating and dropping columns in DataFrames, and applying functions to a column are all extremely useful and used very often in data science.

In addition, our investigation of traffic stops illustrates the wide variety of important data science projects. Projects like this have the potential to influence policy and legislation. Other data science projects can affect development of new medications or therapies, help understand history, or lead to technology like Chat-GPT or Google BARD.

However, many of these projects involve additional statistical and computation skills like machine learning or being able to use large amounts of data from databases. These more advanced topics are what we will cover in Part 2 of this book.

Introduction to Data Science I & II

Investigation

Contents

Investigation#

Traffic Stops#

The Benchmark#

Searches#

Conclusions#