%pip install levenshtein

WARNING: The directory '/home/jovyan/.cache/pip' or its parent directory is not owned or is not writable by the current user. The cache has been disabled. Check the permissions and owner of that directory. If executing pip with sudo, you should use sudo's -H flag.

Collecting levenshtein
  Obtaining dependency information for levenshtein from https://files.pythonhosted.org/packages/1f/22/e41d35e733cd6c3175cbb23e2ce113fa1fc74ffb804165e425ea80a84554/Levenshtein-0.22.0-cp311-cp311-manylinux_2_17_x86_64.manylinux2014_x86_64.whl.metadata

  Downloading Levenshtein-0.22.0-cp311-cp311-manylinux_2_17_x86_64.manylinux2014_x86_64.whl.metadata (3.4 kB)

Collecting rapidfuzz<4.0.0,>=2.3.0 (from levenshtein)
  Obtaining dependency information for rapidfuzz<4.0.0,>=2.3.0 from https://files.pythonhosted.org/packages/fc/5d/c42c05f1de4e604ff69d8c1ee06ee3dcd1b5bf00a396339ade378bb6d5e4/rapidfuzz-3.3.1-cp311-cp311-manylinux_2_17_x86_64.manylinux2014_x86_64.whl.metadata
  Downloading rapidfuzz-3.3.1-cp311-cp311-manylinux_2_17_x86_64.manylinux2014_x86_64.whl.metadata (11 kB)
Downloading Levenshtein-0.22.0-cp311-cp311-manylinux_2_17_x86_64.manylinux2014_x86_64.whl (172 kB)
?25l   ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/172.5 kB ? eta -:--:--
   ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 172.5/172.5 kB 12.7 MB/s eta 0:00:00
?25h

Downloading rapidfuzz-3.3.1-cp311-cp311-manylinux_2_17_x86_64.manylinux2014_x86_64.whl (3.1 MB)
?25l   ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/3.1 MB ? eta -:--:--
   ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 3.1/3.1 MB 134.9 MB/s eta 0:00:00
?25h

Installing collected packages: rapidfuzz, levenshtein

Successfully installed levenshtein-0.22.0 rapidfuzz-3.3.1
WARNING: Running pip as the 'root' user can result in broken permissions and conflicting behaviour with the system package manager. It is recommended to use a virtual environment instead: https://pip.pypa.io/warnings/venv

Note: you may need to restart the kernel to use updated packages.

Sequence-based similarity#

Consider search engines that have indexes of text content. Entering a misspelled search term will match misspellings in the database, but modern search engines often suggest similar queries with larger number of hits in the database. How do they do it? Search engines (like elasticsearch) generate a wide range of possible misspellings of the query and present search results (or spelling suggestions) informed by queries for a comprehensive set of deletion- substitution-, insertion-, and transposition- modified words.

Edit distance (also known as Levenshtein distance) is another approach at fuzzy matching, inspired by the process of changing one input into another. It is more sensitive than Jaccard similarity scoring but requires more computations (that is to say, it takes more time to run when other factors are held constant).

Hamming distance#

If all of the symbols of interest are the same length, say, five-letter telegraph abbreviations, it is simple to count the number of differences letter-by-letter: ENBET differs in one position from ERBET and differs in two positions from TRBET.

This counting-of-differences distance metric goes by the name ‘’Hamming distance’’, but this is suited for vocabularies of aligned codewords all the same length.

Hamming distance would make sense, for instance, comparing dates in ISO-8601 format represented as strings, like “2020-03-15” and “2023-09-21”. Differences of a single character have Hamming distance one; transpositions of digits have Hamming distance 2.

Levenshtein (edit) distance#

If you think about the process of editing text, you can modify text by adding text, deleting text, or, if you are inclined, by both deleting and adding in about the same place. By counting the number of steps needed to transform string1 into string2 using these three operations, deletion, insertion, and substitution, we can define a number that describes how similar the two strings are. There are algorithms that will find the minimum number of edits that will transform one string into another (similar) string and this minimum number of edits score has many uses in data munging.

The Levenshtein distance counts the differences between two strings by describing the minimum number of steps needed to transform one string into the other, where the permitted steps are

substitution (replace a character with a different one)
insertion (add a character), and
deletion.

This is the number of single-character edits needed to transform one string into another.

Levenshtein distance is fairly easy to illustrate by providing an example alignment:

The first string can be changed into the second with a three-character deletion (n't), a three-character substitution (she for you), and eight characters of insertions w and e to go.

The edit distance between the strings is the sum of the number of changes.

Search engines which index text can sometimes give reasonable results when given inexact search queries, but it is not without some engineering. Entering a misspelled search term will match misspellings in the database and will fail to find exact matches on the correct spelling. Modern search engines often suggest similar queries with larger number of hits in the database. How do they do it? Search engines (like elasticsearch) generate a wide range of possible misspellings of the query and present search results (or spelling suggestions) informed by queries for a comprehensive set of deletion- substitution-, insertion-, and transposition- modified words. Yes, you have to check the search index hundreds of times, but if you see a one- or two-letter different search term with hundreds of times the hits, you would do well to suggest it.

import Levenshtein

from Levenshtein import distance

The Levenshtein.distance function finds the minimum number of steps. For two completely different words, all the letters must be replaced:

distance("one", "six")

While for a word that is a subset of another, the missing letters must all be added:

distance("seven", "seventeen")

Distances between number words#

Here we calculate the Levenshtein distance between the words for the first twenty counting numbers in English:

numbers2 = ["one", "two", "three", "four", "five", "six", "seven", "eight", "nine", "ten",
           "eleven", "twelve", "thirteen", "fourteen", "fifteen", "sixteen", "seventeen",
           "eighteen", "nineteen", "twenty"]

d = np.zeros((20,20))
# Calculate distance between all pairs of strings in numbers2
for i in range(len(numbers2)):
    for j in range(len(numbers2)):
        d[i][j] = distance( numbers2[i], numbers2[j])

plt.imshow(d)
plt.colorbar()
plt.title("Levenshtein distance between number words")
plt.yticks(np.arange(len(numbers2)), numbers2, fontsize=6);
plt.xticks(np.arange(len(numbers2)), numbers2, fontsize=6, rotation=90);

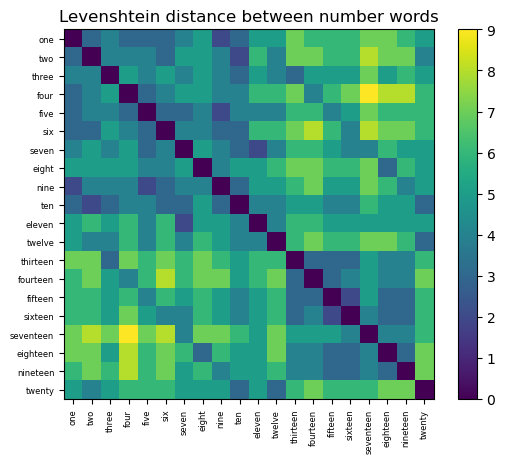
../../_images/Sequence_Based_Similarity_25_0.png

This looks different from the set-based number-word similarity graph we constructed earlier. First, we are measuring distance, not similarity, so the diagonal has distance 0 instead of similarity 1. Second, the range of the distances is integers between 0 and the sum of the lengths of the two strings being compared.

Since this depends on a property of the strings that is not interesting, we can divide by the maximum possible

The calculation of edit distance is, in general, more expensive to calculate than Jaccard similarity or Hamming distance; there are three possible operations at each position, and the operations may need to be repeated.

d2 = np.zeros((20,20))
# Calculate distance between all pairs of strings in numbers2
for i in range(len(numbers2)):
    for j in range(len(numbers2)):
        d2[i][j] = distance( numbers2[i], numbers2[j]) / (len(numbers2[i]) + len(numbers2[j])) 

plt.imshow(1-d2)
plt.colorbar()
plt.title("Levenshtein similarity between number words")
plt.yticks(np.arange(len(numbers2)), numbers2, fontsize=6);
plt.xticks(np.arange(len(numbers2)), numbers2, fontsize=6, rotation=90);

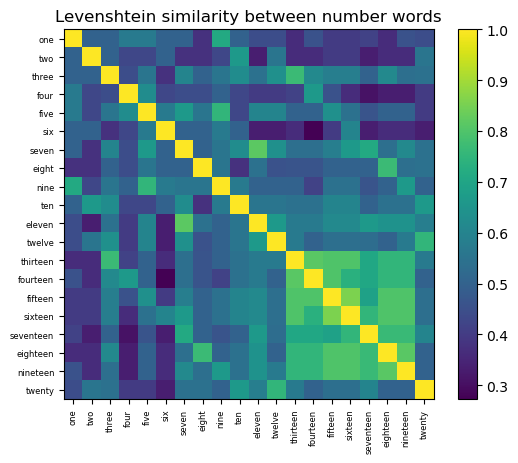
../../_images/Sequence_Based_Similarity_30_0.png

Spelling correction#

One straightforward application of fuzzy matching is spelling correction; after checking each token in a document to see if it is in the dictionary, the words which are not in the dictionary are presented to the user along with suggestions of dictionary words that are similar to the unmatched word.

The fuzzy matching can either start from the misspelled word and generate all possible misspellings out to a certain edit distance, or can start from the words in the dictionary, and find those with the fewest needed edits. Think for a minute which of these might be cheaper (in terms of number of comparisons required.)

words = pd.read_csv("../../data/SINGLE.txt", header=None)

words

	0
0	&c
1	'd
2	'em
3	'll
4	'm
...	...
354979	zymurgy
354980	zythem
354981	zythum
354982	zyzzyva
354983	zyzzyvas

354984 rows × 1 columns

# Start with a special-purpose function that only finds the distance
# to one word of interest: 
word = "wprd"   # This is a misspelling
def dist_to_word(w):
        return distance(w, word)

dist_to_word("worm"), dist_to_word("wierd"), dist_to_word("weird")

(2, 2, 2)

# Check that d(word, word) == 0 
dist_to_word("word") == 0 

False

Check that we can find all the distances in one step:

#note xmode Minimal shortens the error message
%xmode Minimal

Exception reporting mode: Minimal

words[0].apply(dist_to_word)

TypeError: object of type 'float' has no len()

Well, that didn’t work. It seems some of the words in the dictionary aren’t encoded as strings. Let us find the rows that are broken:

def test_str(s):
    return type(s) == str
words[0].apply(test_str)

0         True
1         True
2         True
3         True
4         True
          ... 
354979    True
354980    True
354981    True
354982    True
354983    True
Name: 0, Length: 354984, dtype: bool

badindexes = np.where(words[0].apply(test_str)==False)
badindexes

(array([186010, 186271, 198557]),)

Three rows have non-string names in them.

words.loc[badindexes]

	0
186010	NaN
186271	NaN
198557	NaN

The non-string rows are all encoded as NaN (Not-a-number, a special symbol that acts like a number). Examining the dataframe does not tell us about the source of the problem. Let’s try specifying a data type to read_csv and hope for the best:

words = pd.read_csv("../../data/SINGLE.txt", header=None, dtype="str")

words.loc[badindexes]

	0
186010	NaN
186271	NaN
198557	NaN

That didn’t work either, the bad values are still bad. The documentation for read_csv https://pandas.pydata.org/docs/reference/api/pandas.read_csv.html has a parameter called na_filter that can be turned off.

words = pd.read_csv("../../data/SINGLE.txt", header=None, na_filter=False)

And now we test for bad values:

np.where(words[0].apply(test_str)==False)

(array([], dtype=int64),)

We find none. What were those bad values, now?

words.loc[badindexes]

	0
186010	n/a
186271	nan
198557	null

Huh. Might want to take note of that in the future, some strings, by default, get turned into number-like NaNs.

Now let us find the distances between our word and all the other words:

# define this function in a function that we can use on all the rows in 
# the dictionary: 
def distance_to_all(word):
    def dist_to_word(w):
        return distance(w, word)
    distances = words[0].apply(dist_to_word)
    return distances

distance_to_all("wprd")

0         4
1         3
2         4
3         4
4         4
         ..
354979    6
354980    6
354981    6
354982    7
354983    8
Name: 0, Length: 354984, dtype: int64

Let’s make a new dataframe with the words and the distances to “wprd”:

wprd_dist = words.copy()
wprd_dist["distance"] = distance_to_all("wprd")
wprd_dist

	0	distance
0	&c	4
1	'd	3
2	'em	4
3	'll	4
4	'm	4
...	...	...
354979	zymurgy	6
354980	zythem	6
354981	zythum	6
354982	zyzzyva	7
354983	zyzzyvas	8

354984 rows × 2 columns

Let us examine the histogram of distances. All the words in the dictionary are in there.

wprd_dist.distance.value_counts()

distance
   53564
   50487
   47505
   40228
  38703
  29049
   24864
  21142
  14115
   13233
   8953
   5167
   2858
    2296
   1419
    668
    335
     147
    133
     72
     20
     11
      4
      3
       3
      2
      1
      1
      1
Name: count, dtype: int64

This ordering of the histogram is not ideal for understanding, let us sort by distance:

wprd_dist.distance.value_counts().sort_index()

distance
       3
     147
    2296
   13233
   24864
   40228
   50487
   53564
   47505
  38703
  29049
  21142
  14115
   8953
   5167
   2858
   1419
    668
    335
    133
     72
     20
     11
      4
      3
      1
      2
      1
      1
Name: count, dtype: int64

From the table, which gives the values of edit distance as the index and the number of dictionary words at each distance from our target word as values, we see there are three dictionary words at distance 1, and 147 words at edit distance 2.

wprd_dist.query("distance < 2")

	0	distance
346643	ward	1
350396	wird	1
351455	word	1

wprd_dist.query("distance == 2")

	0	distance
38	3rd	2
15624	aped	2
16021	apod	2
16436	appd	2
16905	apr	2
...	...	...
352228	wur	2
352283	wynd	2
352930	yard	2
353296	yerd	2
353408	yird	2

147 rows × 2 columns

This certainly gives us a starting point (or at least a partly ordered list) of plausible words.

Diffs#

An alignment-based representation of the changes to a document is sometimes an effective way of learning what has changed; algorithms that will compare documents, find the minimum number of edits and show what the edits are with highlighting can be helpful when examining changes to documents or code.

Introduction to Data Science I & II

Sequence-based similarity

Contents