The birthday problem: relaxed assumptions

There are two assumptions we used in the last few sections while investigating the birthday problem - equally likely birthdates and ignoring February 29 as a possible birth date. While relaxing these can complicate the mathematical calculation, the simulations can be easily modified to account for more complicated scenarios.

We use below a dataset from FiveThirtyEight that contains the number of daily births in US between 2000 and 2014 to estimate the odds of each day of the year to be a birthday:

https://github.com/fivethirtyeight/data/tree/master/births

Note that in the following dataset, the variable for day of week is coded 1 for Monday and 7 for Sunday. Also note that there are four leap years in this dataset - finding the correct probability for being born in a leap year is beyond the scope of this section.

birth_data = pd.read_csv("../../data/US_births_2000-2014_SSA.csv")
birth_data

	year	month	date_of_month	day_of_week	births
0	2000	1	1	6	9083
1	2000	1	2	7	8006
2	2000	1	3	1	11363
3	2000	1	4	2	13032
4	2000	1	5	3	12558
...	...	...	...	...	...
5474	2014	12	27	6	8656
5475	2014	12	28	7	7724
5476	2014	12	29	1	12811
5477	2014	12	30	2	13634
5478	2014	12	31	3	11990

5479 rows × 5 columns

This is an interesting dataset and we encourage you to use it to answer questions like: what is the least frequent day of the week for giving birth?

The pandas library has commands that allow you to group rows by unique values in a column. We introduced it in Chapter 7.

counts_df=birth_data.groupby(['month','date_of_month']).sum()[['births']]
counts_df.head(5)

		births
month	date_of_month
1	1	116030
	2	144083
	3	170115
	4	171663
	5	166682

We see that there were 116,030 births on January 1st, 144,083 (much larger! why?) on January 2nd etc. A histogram of the counts in the above data frame:

plt.hist(counts_df.births,bins = np.arange(116000, 195000, 2000))
plt.xticks(ticks=[130000,150000,170000,190000], labels=["130K","150K","170K","190K"])
plt.xlabel("Number of births");

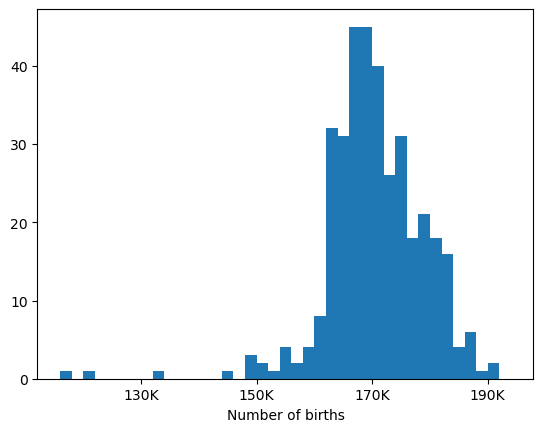
Note that some days of the year are outliers in number of births. Can you guess which?

We will use these counts to estimate the probability that a given date is a birthday for a random US subject.

bday_probs=counts_df.births/sum(counts_df.births)

These probabilities are added to the simulation when using the random.choice function. Look at the function below and compare it to the birthday_sim function introduced in Section 11.2.

# adding February 29 - the number of possible birthdays is now 366
birthdays2=np.arange(1,367,1)

def birthday_sim2(n,nrep,pr):
    '''Estimate birthday matching probabilities using nrep simulations.
       The 366 possible birthdays are weighted by given probabilities'''
    outcomes = np.array([])
    for i in np.arange(nrep):
        outcomes = np.append(outcomes,
                Counter(np.random.choice(birthdays2,n,p=pr)).most_common(1)[0][1])
    return outcomes

We calculate below the probability for the case \(n=23\) using these relaxed assumptions. Before running the cell or reading its output, do you think the probability will be higher or lower?

n=23
nrep=100000
sum(birthday_sim2(n,nrep,bday_probs)>1)/nrep

0.50871

Note: more accurate simulation experiments do not always lead to different results - but we do not know that before performing them!

We will continue to investigate the issue of analytical and computation approaches throughout this textbook.